2025年九月即将踏入集成电路学习之旅,为接下来研究高速电路打好坚实的基础,决定提前学习好电路的一些基础知识,并注重知识的直觉化形成,我坚信知识形成直觉后运用起来就像自己的四肢五感一般丝滑,接下来的博客我将记录下自己学习的一些心得,同时附上自己看到的知识的来源。
分析电路遇到的第一个与直觉相悖的事实就是除了初中便学过的电阻居然有复数形式的阻抗,并且能使用欧拉公式()的样子来表达,这简直令人难以理解。电阻的定义是电压除以电流,再熟悉不过了,怎么会凭空出现个复数的样子,为什么分析正弦电路时要引入相量,相量的两个分量又有什么实际意义? - 知乎在时域上正弦带相位的时间函数转换到频域上时会出现一个复数,这个复数表示了频域上相位的改变eiθ,(并不是说cosθ就是eiθ,而是说cosθ可以用eiθ+e-iθ表示,将拉普拉斯变换后解复变量方程得到的复平面上的所有复数还原成复指数信号相加,再还原即得到我们喜闻乐见得cosθ和sinθ的形式。
由傅里叶变换【硬核】工科生苦傅里叶久矣!傅里叶变换原理究极入门,工科生的必修课,看不懂的来找我算账!【喵星考拉】傅里叶变换究极入门课程_哔哩哔哩_bilibili 形象化解释【官方双语】形象展示傅里叶变换_哔哩哔哩_bilibili(考拉的视频讲解了傅里叶变换到频域的思想是将两个函数看作无穷维的向量做内积得到的投影,3blue的视频解释了投影的计算过程,将f(t)一圈圈绕在eiωt上得到的复数向量做积分得到的结果是一个复数,这个复数包含了信号的幅度,相位,频率信息,之所以积分得到相位信息是因为原本的sinθ经过在一个周期内的e-iωt内积积分得到的复向量刚好落在负半轴上,如果在无穷周期也没差,由于欧拉公式旋转的周期特性,即使在无穷周期上积分仍然能捕捉其三角信号的相位信息)们知道任何时域上的信号都可以转变为频域的一个函数,这个函数若是由ωi作为输入量,则输出是对应ωi上的一个复数,这个复数包含信号的相位信息,幅度大小,如果是拉普拉斯变换,则是引入了衰减系数的傅里叶变换,意味着这个函数是由α+ωi作为输入量,输出同样是对应复平面上的一个复数,这个复数包含衰减系数,频率大小,相位信息,幅度大小四维变量。
拉普拉斯变换有什么用呢,先说它的计算方法,一是含有复变量的函数(符合柯西黎曼等式,雅可比矩阵)可以按照正常的实变函数求导积分原则得出来个复数的函数,二是通过欧拉公式将其拆开为实部虚部的函数。再说他得出来的复数的性质,这个复数就是相量,所在的坐标轴是一个包含所有初始状态的复平面由s表示,虚轴显示所有的ω,实轴显示所有衰减系数,相量表示了在衰减系数σ下一个频率ω的正弦波放大(缩小)了多少倍数以及相位角是多少,当得出的复数在这个ω和σ下为无穷大时,意味着这个信号经过拉氏变换找到的这个频率在这个衰减系数下就是刚好不收敛了(所谓的极点要求所有的信号叠加项满足σ右边的交集),某个变量拉式变换得到频域上复数的函数,某个变量时域上的微分在σ为零的频域上的相对于原变量仅相当于旋转,这时的我们已经知道时域的信号可以由est线性组合,那么微分就是乘一个复数s减去初值信号,积分就是除个s,时域上的时移等于频域上的相移(一个正弦信号向右移动实质上是在对应在频域上的复数旋转了,旋转了九十度则从实部到虚部或从虚部到实部,旋转45度则则可知实部有正弦信号,虚部有余弦信号,且根据高中数学的三角合成公式可知45度正弦信号可以拆成两个幅度一样的正弦余弦信号,在频域图上也确实是这样的
浅谈微分方程与线性代数的联系 微分方程的直觉联系 https://www.bilibili.com/video/BV1tb411G72z/)自由响应和强迫响应,微分方程【硬核】工科生都逃不掉的拉氏变换,居然又炫酷又实用|拉普拉斯变换原理、图解与应用,傅里叶变换进阶,控制理论必修课【喵星考拉】_哔哩哔哩_bilibili,微分方程如简谐运动列出的方程为什么说有振动的地方就有特征值 实质上求解的是这个无穷维矩阵的特征向量,对于一个二阶线性微分方程,它的解我们已经默认的知道是e-st了,然后接触两个数,有特解就三个
待解的问题:冲激函数的拉氏变换为1相乘于传递函数与冲激函数与单位脉冲响应做卷积得出得结果为什么一样,频域上理解,输出脉冲响应是由输入脉冲响应通过传递函数加权得到(这是傅里叶变换的精髓,只要调整正余弦函数的系数和相位就能变换成任意的函数)而冲激函数能拉氏变换出所有的频率成分且均为1,在频域上乘了一等于没变,在时域上首先有冲激响应导致单位脉冲响应的定义,其次冲激响应经过线性时不变系统(相当于卷积运算)得出的就是单位冲激响应,一个连续的时间信号可以表示为加权移位的冲激函数响应的叠加,卷积积分就是任意函数经过线性时不变系统,再那就可以得出时域上的卷积运算和
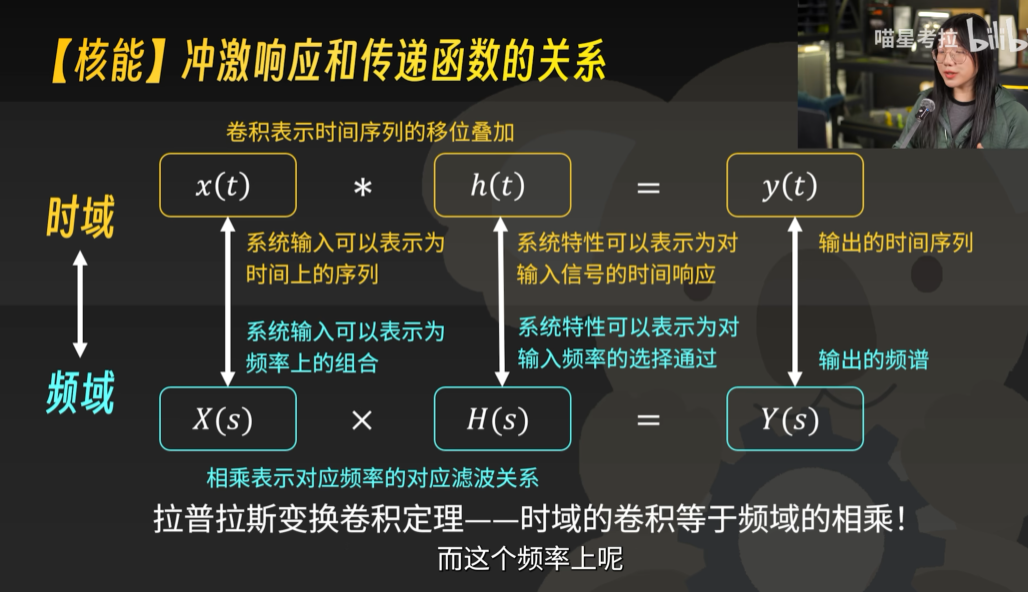
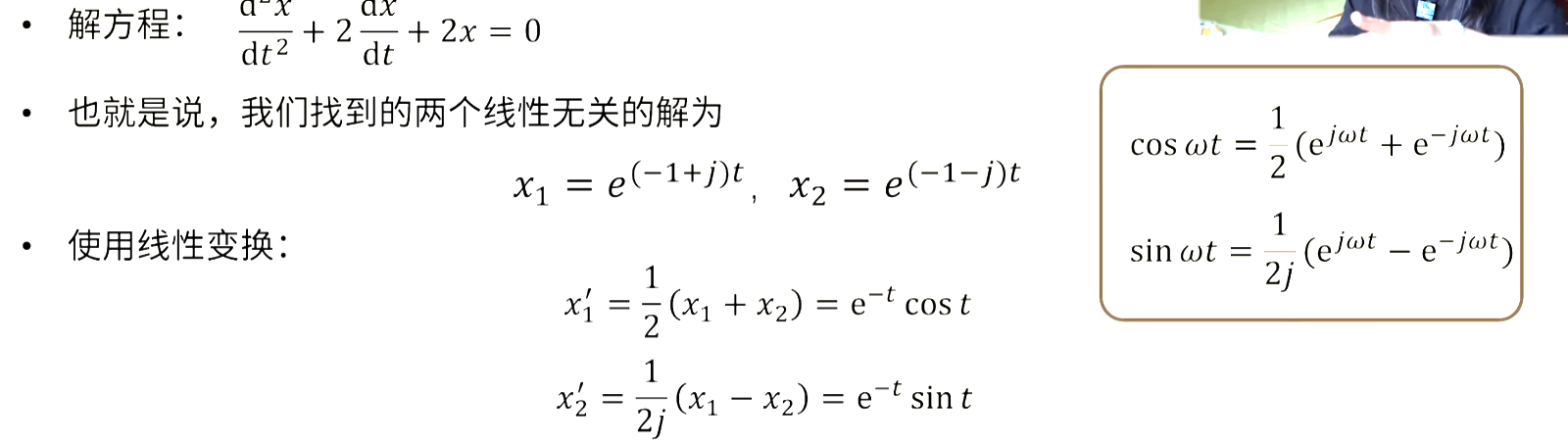
拉普